Lab 05: Advanced A2C
Goals
- Support continuous action
- Incorporate entropy loss
- Leverage GAE
Overall, we will tackle a more challenging task - Pendulum-v0.
Continuous Action Support
Different from the deterministic policy of DDPG, A2C uses stochastic policy,
i.e., it outputs a distribution. Usually, we use the Gaussian distribution to
model the action policy. Specifically, given an observation \(obs\), assuming
our act network is \(act\_net(\cdot)\), the output of the policy should be
\(\mu\) and \(\theta\), which is the mean and variance of a Gaussian
distribution. Then, an action can be sampled from the distribution
\(\mathcal(N)(\mu,\theta)\). Since the dimensions of both \(\mu, \theta\) are as
same as the action dimension, your act_net may look like this:
self.act_net = nn.Sequential(
nn.Linear(n_state, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU(),
nn.Linear(128, 2*n_action),
)
When you use the act_net to output an action, it will be something like this:
from torch.distributions.normal import Normal
...
def __call__(self, state):
with torch.no_grad():
state = torch.FloatTensor(state).to(device)
output = self.act_net(state)
mu = self.act_lim*torch.tanh(output[:n_action])
var = torch.abs(output[n_action:])
dist = Normal(mu, var)
action = dist.sample()
action = action.detach().cpu().numpy()
return np.clip(action, -self.act_lim, self.act_lim)
As you can see, we manually divide the output of the act_net into mean and variance. Note that we need to make sure the variance always positive. Therefore, we put abs() around it. Also, mu is regulated with tanh to produce smooth output.
When calculating the log probabilities for estimating loss, we follow the same intuition to manually extract mu and var. Then we can form a Normal distribution and calculate the corresponding log probability of an action act given mu and var. The code looks like this:
logprob = dist.log_prob(act).squeeze_()
Note that when converting act from numpy to tensor, make sure the type is FloatTensor not LongTensor (which is for discrete action).
After making the modification, you should be able to run the code but expectedly with poor performance. Because we don’t have effective exploration strategy.
Incorporate Entropy Loss
Take a quick look at this Wiki page to get a brief idea of entropy. Basically, it measures the randomness of an event. In the context of our policy, the greater the entropy is, the more uncertain it behaviors. Incorporating entropy into loss can help with exploration by encouraging some degree of randomness in the policy.
Mathematically, given a Gaussian distribution with known \(\mu\) and \(\theta\), the entropy can be calculated with the formula HERE. Thankfully, Pytorch has a build-in function to help us. Therefore, the entropy loss can be calculated as
ent_loss = dist.entropy().mean()
Keep in mind that we want ent_loss to be large, NOT small. Also, don’t forget
to put a coefficient on ent_loss when adding to the total loss. A good setting
for me is 0.01.
Leverage GAE
Read these articles to understand what is GAE
- RL — Policy Gradients Explained (Part 2)
- Generalized Advantage Estimate: Maths and Code
- Notes on the Generalized Advantage Estimation Paper (Feel free to skip the mathy propositions and proofs)
- Sample Code
Feel free to adapt the sample code to calculate GAE.
Tips to calculate GAE
When calculating advantages, you need to use your value network v_net(). In order to stabilize the training, we want to fix the advantages when updating parameters. More specifically, in each training cycle (after collecting one episode of data), we need to make sure the advantages are constant. In other words, while v_net will keep changing after each batch update, we don’t want to calculate advantages using the changing v_net. Instead, , we want to calculate advantages using the v_net before any update in this round.
Set gae_lambda = 0.85 for initial setting.
This technique is very similar to the target network used in DQN. In order to do this, feel free to create another value network called old_v_net as this:
import copy
self.old_v_net = copy.deepcopy(self.v_net)
self.old_v_net.to(device)
Then before updating in each round, record the current v_net as old_v_net
for i in tqdm(range(3000)):
data = run_episode(env, agent)
agent.old_v_net.load_state_dict(agent.v_net.state_dict())
for _ in range(5):
loss_act, loss_v, loss_ent = agent.update(data)
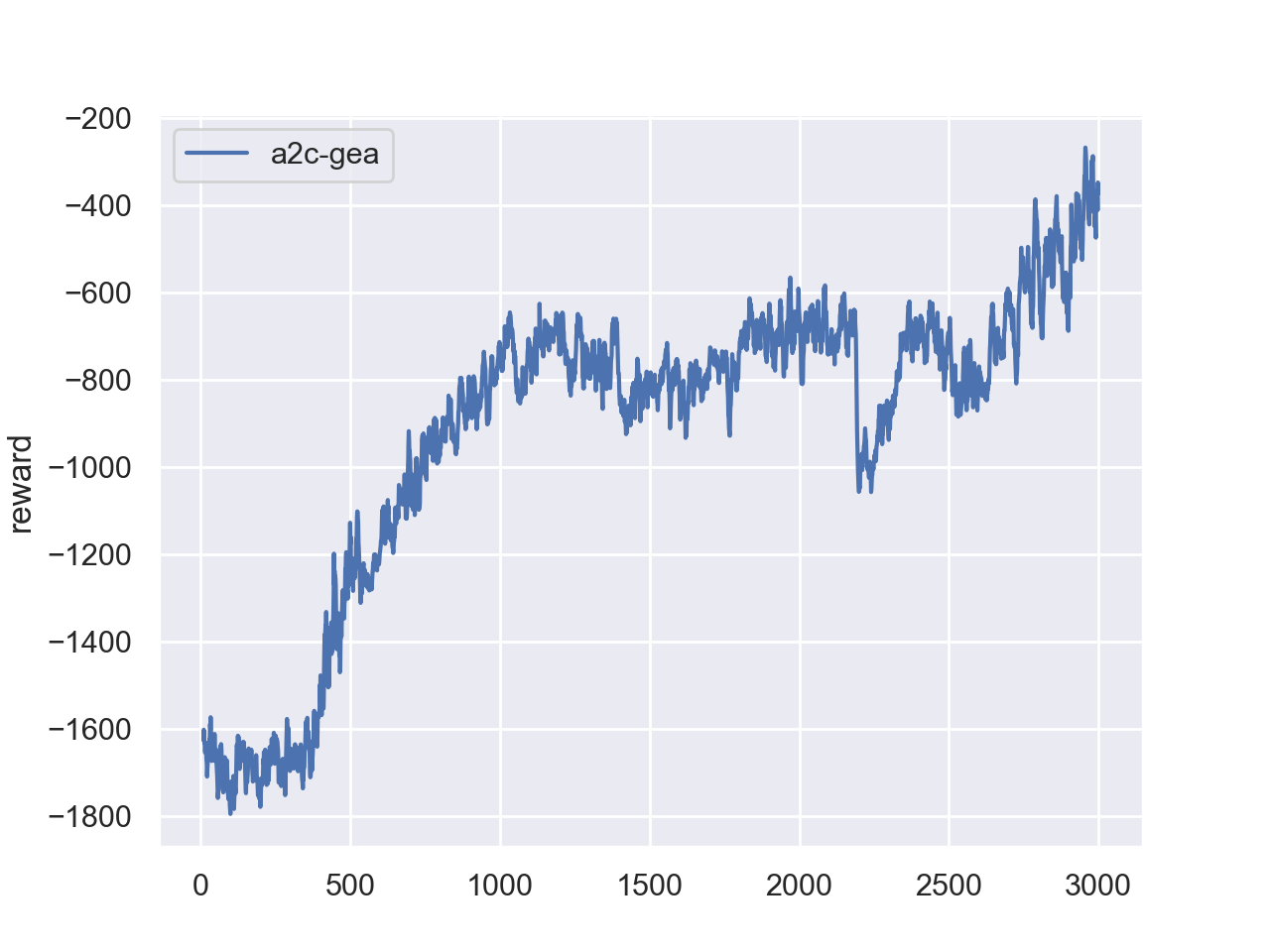
Expected Performance
Environment: Pendulum-v1
Target: Peak reward > -300 (average over 100 test episodes)
Typical Training Progress:
- Episodes 0-100: Reward -1000 to -500 (high variance, exploration phase)
- Episodes 100-300: Reward -500 to -300 (gradual improvement)
- Episodes 300-500: Reward -300 to -200 (converging)
- Episodes 500+: Stabilized around -200 to -300
Note: A2C has inherently high variance - seeing oscillations is normal. Use moving average (last 50 episodes) to assess true performance.
Grading Criteria (15 pts for performance):
- Full credit: Peak reward > -300 (shows good learning)
- Partial credit: Reward > -600 (shows some learning)
- Minimal credit: Reward > -900 (minimal threshold)
GAE Lambda Impact:
- λ = 0.7: Faster but higher variance
- λ = 0.85: Balanced (recommended)
- λ = 0.99: Slower but more stable
- You should see these trade-offs in your experiments
Write Report
- Run the program with three
gae_lambdasettings:0.7,0.85,0.99. Record the training log from the three setup and plot the reward curves. - Write your observation/insight on the impact of
gae_lambda.
Deliverables and Rubrics
Overall, you need to complete the environment installation and be able to run the demo code. You need to submit:
- (70 pts) A PDF from running the your code in jupyter notebook with accuracy reported in the program output.
- (15 pts) Performance: The peak of reward reaches above -900.
- (15 pts) Reasonable answers to the questions (backed up with experiment results)
Debugging Tips
My network setup:
self.act_net = nn.Sequential(
nn.Linear(n_state, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU(),
nn.Linear(128, 2*n_action),
)
self.act_net.to(device)
self.v_net = nn.Sequential(
nn.Linear(n_state, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU(),
nn.Linear(128, 1),
)
self.v_net.to(device)
self.v_optimizer = torch.optim.Adam(self.v_net.parameters(), lr=1e-3)
self.act_optimizer = torch.optim.Adam(
self.act_net.parameters(), lr=1e-4)
Notice that I use slower learning rate for act_net. The intuition is that, the
update of v_net depends heavily on the quality of trials. Bad trial data can
shift v_net to bad value thus further misguiding act_net to update toward
bad policy. Therefore, having slower act_net helps take conservative update
according to the current v_net.
The structure of update() function looks like this:
# Calculate stuff before this
batch_size = 32
list = [j for j in range(len(obs))]
for i in range(0, len(list), batch_size):
index = list[i:i+batch_size]
for _ in range(1):
#calculate act_loss
ent_loss = dist.entropy().mean()
act_loss -= 0.01*ent_loss
self.act_optimizer.zero_grad()
act_loss.backward()
self.act_optimizer.step()
for _ in range(1):
#calculate v_loss
self.v_optimizer.zero_grad()
v_loss.backward()
self.v_optimizer.step()
return act_loss.item(), v_loss.item(), ent_loss.item()
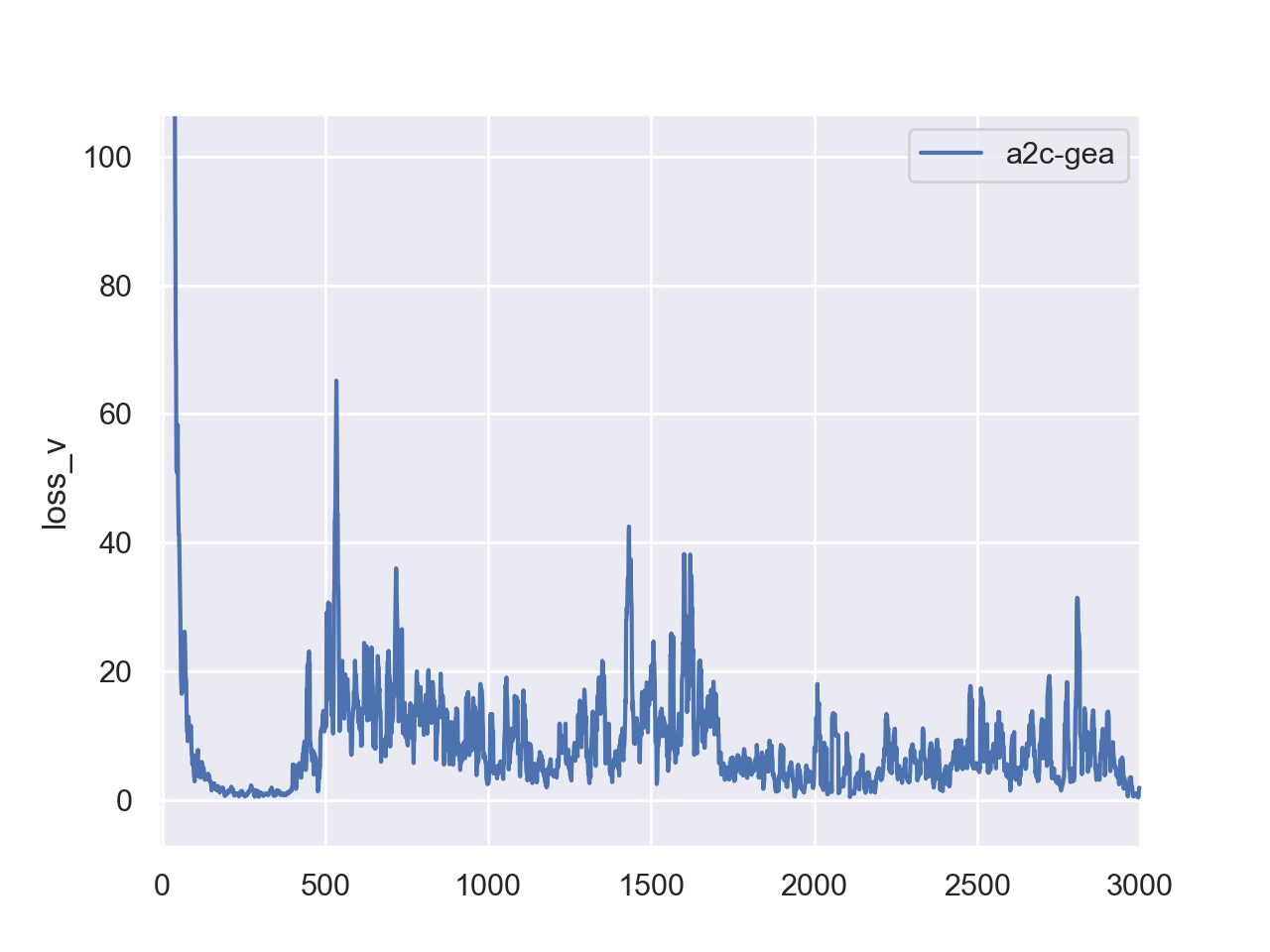
If your v_loss looks very large (thousands to ten thousands), first thing you
want to check is the discount factor self.gamma. Large gamma can introduce
large variance therefore reducing gamma, say to 0.95, helps reduce v_loss.
Second, you may want to change the way to calculate TD_target when training
v_net. TD(infinite), i.e., MC, can lead to high v_loss. Try to change it
to TD(0) to see if performance got improved.
My training curves are like: